Страница 2

 

4000 лет спустя

 

История теоремы Пифагора уходит в глубокую древность.

 

Упоминания о ней содержатся ещё в вавилонских клинописных текстах времён царя Хаммурапи (XVIII век до н. э.), то есть за 1200 лет до рождения Пифагора.

 

Теорема применялась как готовое правило во многих задачах, самая простая из которых — нахождение диагонали квадрата по его стороне.

 

Не исключено, что соотношение a² + b² = c² для произвольного прямоугольного треугольника вавилоняне получили, попросту «обобщив» равенство a² + a² = c². Но им это простительно — для практической геометрии древних, сводившейся к измерениям и вычислениям, строгих обоснований не требовалось.

 

Теперь, почти 4000 лет спустя, мы имеем дело с теоремой-рекордсменом по количеству всевозможных доказательств. Между прочим, их коллекционирование — давняя традиция.

 

Пик интереса к теореме Пифагора пришёлся на вторую половину XIX — начало XX столетия. И если первые коллекции содержали не более двух-трёх десятков доказательств, то к концу XIX века их число приблизилось к 100, а ещё через полвека превысило 360, и это только тех, что удалось собрать по разным источникам.

 

Кто только не брался за решение этой нестареющей задачи — от именитых учёных и популяризаторов науки до конгрессменов и школьников. И что примечательно, в оригинальности и простоте решения иные любители не уступали профессионалам!

 

Самым древним из дошедших до нас доказательствам теоремы Пифагора около 2300 лет.

 

Одно из них — строгое аксиоматическое — принадлежит древнегреческому математику Евклиду, жившему в IV—III веках до н. э. В I книге «Начал» теорема Пифагора значится как «Предложение 47».

 

Самые наглядные и красивые доказательства построены на перекраивании «пифагоровых штанов». Они выглядят как хитроумная головоломка на разрезание квадратов. Но заставьте фигуры правильно двигаться — и они откроют вам секрет знаменитой теоремы.

 

Вот какое изящное доказательство получается на основе чертежа из одного древнекитайского трактата (рис. 3), и сразу проясняется его связь с задачей об удвоении площади квадрата.

 

 

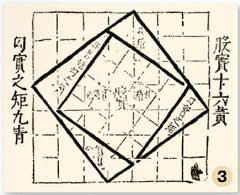
Именно такое доказательство пытался объяснить своему младшему другу семилетний Гвидо, не по годам смышлёный герой новеллы английского писателя Олдоса Хаксли «Маленький Архимед».

 

Любопытно, что рассказчик, наблюдавший эту картину, отметил простоту и убедительность доказательства, поэтому приписал его... самому Пифагору. А вот главный герой фантастической повести Евгения Велтистова «Электроник — мальчик из чемодана» знал 25 доказательств теоремы Пифагора, в том числе данное Евклидом; правда, ошибочно назвал его простейшим, хотя на самом деле в современном издании «Начал» оно занимает полторы страницы!

 

Первый математик

 

Пифагора Самосского (570—495 годы до н. э.), чьё имя давно и неразрывно связано с замечательной теоремой, в известном смысле можно назвать первым математиком.

 

Именно с него математика начинается как точная наука, где всякое новое знание — результат не наглядных представлений и вынесенных из опыта правил, а итог логических рассуждений и выводов. Лишь так можно раз и навсегда установить истинность любого математического предложения.

 

До Пифагора дедуктивный метод применял только древнегреческий философ и учёный Фалес Милетский, живший на рубеже VII—VI веков до н. э. Он высказал саму идею доказательства, но применял его не систематически, избирательно, как правило, к очевидным геометрическим утверждениям типа «диаметр делит круг пополам».

 

Пифагор продвинулся гораздо дальше. Считается, что он ввёл первые определения, аксиомы и методы доказательства, а также создал первый курс геометрии, известный древним грекам под названием «Предание Пифагора». А ещё он стоял у истоков теории чисел и стереометрии.

 

Другая важная заслуга Пифагора — основание славной школы математиков, которая более столетия определяла развитие этой науки в Древней Греции.

 

С его именем связывают и сам термин «математика» (от греческого слова μαθημa — учение, наука), объединивший четыре родственные дисциплины созданной Пифагором и его приверженцами — пифагорейцами — системы знаний: геометрию, арифметику, астрономию и гармонику.

 

Отделить достижения Пифагора от достижений его учеников невозможно: следуя обычаю, они приписывали собственные идеи и открытия своему Учителю. Никаких сочинений ранние пифагорейцы не оставили, все сведения они передавали друг другу устно.

 

Так что 2500 лет спустя историкам не остаётся ничего иного, кроме как реконструировать утраченные знания по переложениям других, более поздних авторов.

 

Отдадим должное грекам: они хоть и окружали имя Пифагора множеством легенд, однако не приписывали ему ничего такого, чего он не мог бы открыть или развить в теорию. И носящая его имя теорема не исключение.